Decision trees explained using Weka
Decision trees are a classic supervised learning algorithms, easy to understand and easy to use. In this article we will describe the basic mechanism behind decision trees and we will see the algorithm into action by using Weka (Waikato Environment for Knowledge Analysis).
Decision trees
The main concept behind decision tree learning is the following: starting from the training data, we will build a predictive model which is mapped to a tree structure. The goal is to achieve perfect classification with minimal number of decision, although not always possible due to noise or inconsistencies in data.
Here is a sample training data set – we are trying to predict the success of movie taking into consideration features like: country of origin, if big stars are playing and the movie’s genre.
| CountryOfOrigin | BigStar | Genre | Success/Failure |
|---|---|---|---|
| USA | yes | scifi | Success |
| USA | no | comedy | Failure |
| USA | yes | comedy | Success |
| Europe | no | comedy | Success |
| Europe | yes | scifi | Failure |
| Europe | yes | romance | Failure |
| Australia | yes | comedy | Failure |
| Brazil | no | scifi | Failure |
| Europe | yes | comedy | Success |
| USA | yes | comedy | Success |
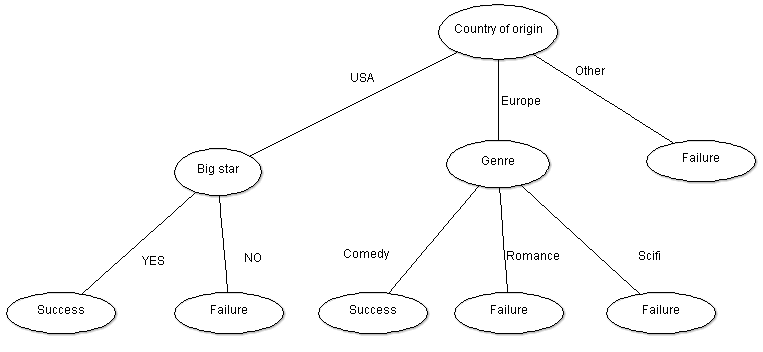
From this table we need a decision tree which can be used to predict the success or failure of a new film. A decision tree learning algorithm will return a predictive model which could be graphically represented as following:
As you can see, each level splits the data according to different attributes, the non-leaf nodes are represented by attributes, the leaf nodes represent the predicted variable – in our case Success or Failure.
The basic algorithm for learning decision trees is:
- starting with whole training data
- select attribute or value along dimension that gives “best” split
- create child nodes based on split
- recurse on each child using child data until a stopping criterion is reached: all examples have same class or the amount of data is too small or the tree is too large
The main challenge while building the tree is to decide on which attribute to split the data at a certain step in order to have the “best” split. The answer for this is the information gain concept. Information gain is the difference between the entropy before and after a decision. Entropy is a measure of the uncertainty contained in a piece of information (the concept was also explained in this article https://technobium.com/sentiment-analysis-using-opennlp-document-categorizer/). In our example, we must select the attribute which lowers the entropy. The formula for the entropy is the following:
Entropy = -pP * log2(pP) -pN * log2(pN)
pP – the proportion of positive (training) examples
pN – the proportion of negative (training) examples
Going back to the example, the initial entropy is 1 because there are 5 successes and 5 failures. The algorithm will start with calculating the information gain for splitting the data by the attribute “CountryOfOrigin”:
- Entropy(USA) = -0.75 * log2(0.75) – 0.25 * log2(0.25) = 0.811
- Entropy(Europe) = 1.0 (2 of each)
- Entropy(Other) = 0.0 (2 Failures)
- Entropy(CountryOfOrigin) = 0.4 * 0.811 + 0.4 * 1.0 + 0.2 * 0.0 = 0.7244
- Information Gain(CountryOfOrigin) = 1.0 – 0.7244 = 0.2756
After calculating in a similar manner for the remaining attributes we will have:
- Information gain for “BigStar” attribute = 0.03
- Information gain for “Genre” attribute = 0.16
Because the information gain for “CountryOfOrigin” is the biggest (0.2756 vs 0.03 vs 0.16), this is the first node in the decision tree.
The algorithm continues to build the decision tree, by evaluating the remaining attributes under the initial branches.
Decision tree learning with Weka ID3
A popular decision tree building algorithm is ID3 (Iterative Dichotomiser 3) invented by Ross Quinlan. Weka has implemented this algorithm and we will use it for our demo.
But first, a few words about Weka: Waikato Environment for Knowledge Analysis (Weka) is a popular suite of machine learning software written in Java, developed at the University of Waikato, New Zealand. It is free software licensed under the GNU General Public License. Weka offers a workbench that contains a collection of visualization tools and algorithms for data analysis and predictive modeling, together with graphical user interfaces for easy access to these functions. Beside that, it offers also Java library which can be used independently.
Download and install Weka from here http://www.cs.waikato.ac.nz/ml/weka/downloading.html. After that you will need the training data found in the following archive: films. Inside the archive there is a “films.arrf” file ( for more details about the ARRF file format see here http://www.cs.waikato.ac.nz/ml/weka/arff.html).
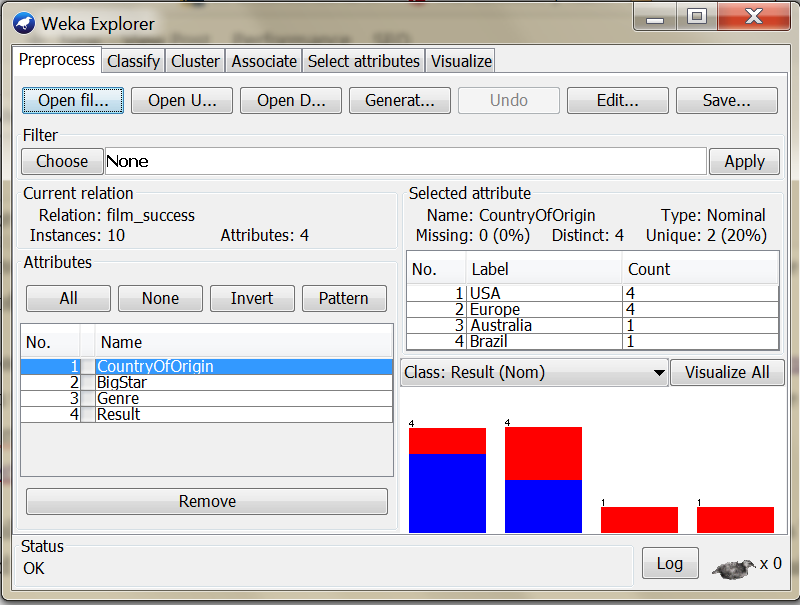
Let’s build the decision tree using the Weka Explorer. From the “Preprocess” tab press “Open file” button and load the “films.arrf” file downloaded previously. You should see something similar to this:
Go then to the “Classify” tab, from the “Classifier” section choose “trees” > “ID3” and press Start.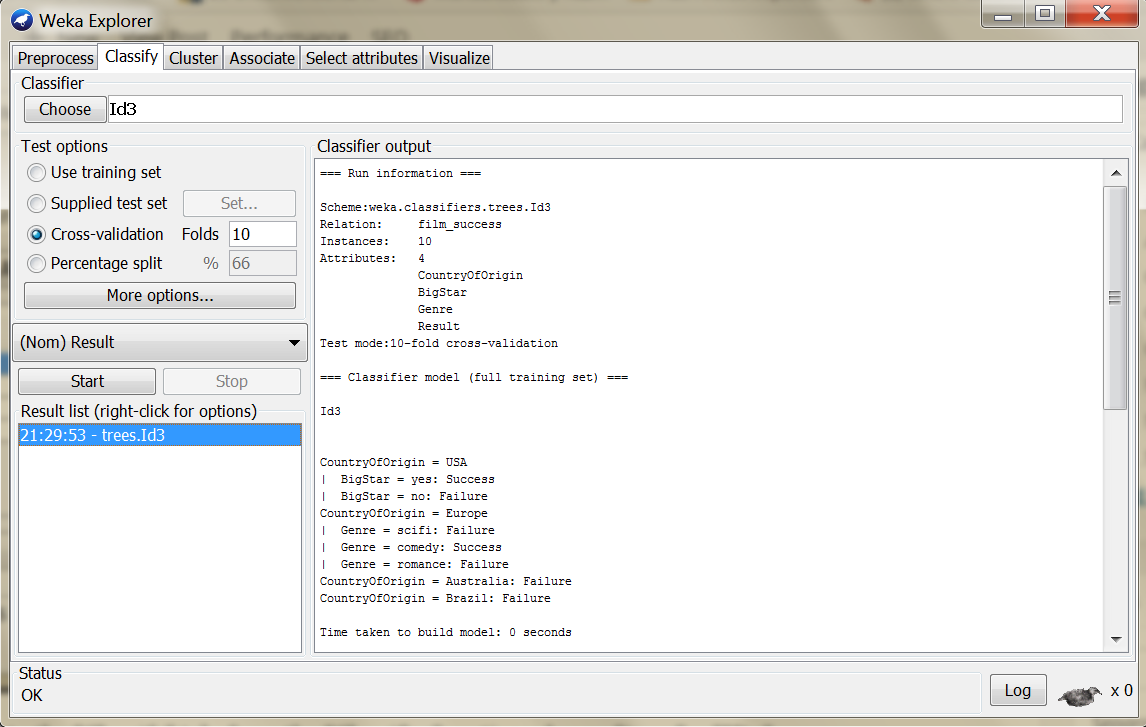
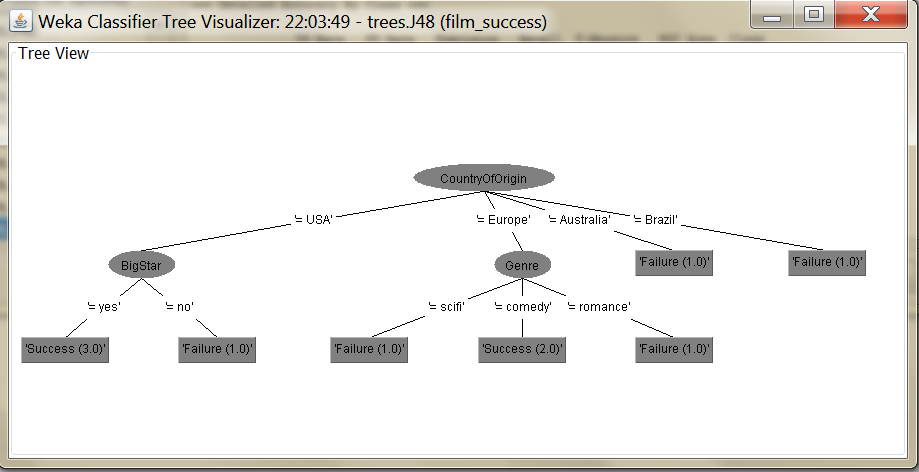
For the moment, the platform does not allow the visualization of the ID3 generated trees. The J48 decision tree is the Weka implementation of the standard C4.5 algorithm which is the successor of ID3. Weka allow sthe generation of the visual version of the decision tree for the J48 algorithm. So, from the “Classifier” section select “trees” > “J4.8”. Also make sure that the “-C 0.25 -M 1” options are selected for the algorithm. There options represent:
- confidenceFactor — The confidence factor used for pruning (smaller values incur more pruning).
- minNumObj — The minimum number of instances per leaf.
Press again “Start”. After the calculation select the result in the left pane, right-click and select “Visualize tree”.
As you see, the generated decision tree is similar to the one at the top of the article.
Java version of the algorithm
As mentioned before, besides the visualization workbench, Weka offers also a Java library which can be used in third party applications. On GitHub you can find the Java project which build the ID3 decision tree programmatically, starting from the same training data file: https://github.com/technobium/weka-decision-trees
By running the Java code you should obtain the following result:
Id3 CountryOfOrigin = USA | BigStar = yes: Success | BigStar = no: Failure CountryOfOrigin = Europe | Genre = scifi: Failure | Genre = comedy: Success | Genre = romance: Failure CountryOfOrigin = Australia: Failure CountryOfOrigin = Brazil: Failure ----------------------------------------- Test data : Europe,no,comedy Test data classification: Success
Conclusion
Decision trees are a easy to use and easy to understand supervised learning algorithms class. They are used successfully for the following type of problems:
- loan applications
- medical diagnosis
- movie preferences
- spam filters
- security screening
Decision trees perform well with large datasets and can handle both numerical and categorical data. They are also at the base of random forests.
References
http://www.cs.miami.edu/home/geoff/Courses/COMP6210-10M/Content/DecisionTrees.shtml
https://www.cs.cmu.edu/afs/cs/academic/class/15381-s07/www/slides/041007decisionTrees1.pdf





Great work Leo. I am developer in Eclat Technosoft. Your blog is useful for me. I am searching for the java code for CART algorithm using Weka Jar. I can see many trees under( weka.classifiers.trees.) jar file. but i cant get CART on this.
Can you help me regarding this?